In this article, I will try to explain the notation log N while calculating time complexity of an algorithm. We all know that to find an element in an array we need to iterate through the array of elements and compare it with the required value. In the case of searching for an element on the worst case i.e, the element is found to be the last element we end up in iterating through all the elements in the array as shown in Fig 1. Hence, in the worst case searching an element in an array, we have to do number of comparison which is equal to the number of elements in the array. Therefore, the worst case time complexity for search for an element in an array is linear or the worst case time taken to search for an element in an array is directly proportional to the size of the array.
Time complexity to search for an element in an array = O(N)
Where, N is number of elements in an array.
While sorting elements in an array with a naive approach, every elements has to be compared with every other elements in the array as shown in Fig 2. Hence, the time complexity of sorting an array is number of elements in the array multiplied by number of elements in the array. Therefore, the time complexity of sorting an array of elements is quadratic or the time taken to sort an array is directly proportional to the square of number of elements in the array.

Time complexity of sorting an array = O(N x N)
Where, N is number of elements in an array.
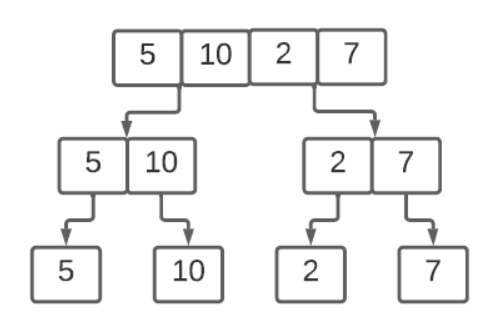
One of the approaches to reduce the time complexity of sorting is divide and conquer approach. Merge sort algorithm is one of the algorithms that uses divide and conquer approach. In merge sort, the array is divided into two arrays, further these two arrays are again divide into four arrays until we have arrays with size of 1 as shown Fig 3. The above describes the divide part of the divide and conquer approach. The next part is merging the arrays to form a single array.
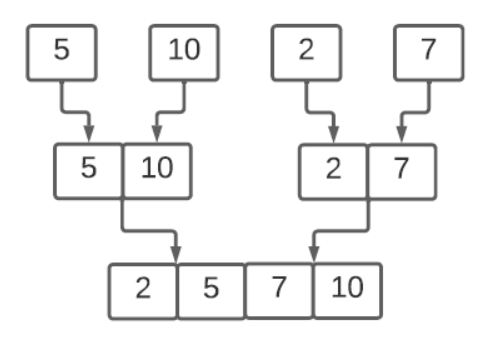
While merging, the two arrays are compared and merged into a single sorted array. Later the merged array is again merged with another merged array to form another merged array. The process continues until all the arrays are merged as shown in Fig 4.
While dividing the array, the array is divided many times, the number of times the array is divided is equal to number of times the size of the array has to be divided by two to get 1. This is what logarithm is about, logarithm gives number of times you can divide the number by the base. In our case base is two and the number is size of the array. Therefore, the time complexity to divide the arrays is logarithm of the number of elements in the array.
Time complexity to divide array recursively to form arrays with single elements = O(log N).
Where, N is number of elements in an array.
As explained above, the number times arrays are merged is equal to number of times the size of the original array has to be divided by two to get 1. But, while merging at each merge level we have to do many comparisons. The number of comparison is equal to the size of the original array. Hence, the time complexity of merging is multiple of number of elements in the original array and logarithm of the number of elements in the original array.
Time complexity to merge arrays recursively
to form single array = O(N log N).
Where, N is number of elements in an array.
The overall time complexity of sorting an array is sum of time complexity to divide the array and merge the array. Time complexity of sorting an array is O(log N) + O(N log N). Since O(N log N) > O(log N), the O(log N) is neglected. Therefore, the overall time complexity of sorting an array is O(N log N).
Mathematical Proof:
The time complexity to divide an array into two is 1. Hence the time complexity to divide an array with n elements into arrays of single element is given below:
T(N) = 2 * T(N/2) + 1
Where, T(N) time complexity to divide an array with N elements.
The above can be rewritten as:
T(N) = 4 * T(N/4) + 2 or,
T(N) = 2^a * T(N/2^a) + a
Let us assume a = log N then,
T(N) = 2^log N * T(N/2^ log N) + log N
T(N) = N * T(N/N) + N = N * T(1) + log N
Since, the time complexity to divide array with single element is Zero, T(1) = 0.
Therefore,
T(N) = log N
The time complexity to compare while merge two arrays at each level of merging is equal to number of element in original array. Hence the time complexity to merge arrays into an arrays is given below:
T(N) = 2 * T(N/2) + N
T(N) is time complexity to merge N single element arrays to single sorted array.
Applying same Technic as before,
T(N) = 2^a * T(N/2^a) + a * N
Assuming a = log N
T(N) = 2 ^ log N * T(N/2^log N) + log N * N
T(N) = N * T(N/N) + N log N
T(N) = N * T(1) + N log N
But, Time complexity to merge one array is Zero as it need not be merged, T(1) = 0
T(N) = N log N
As already discussed, we now have mathematical proof that,
Divide time complexity = O(log N)
Merge time complexity = O(N log N)
The overall time complexity is O(N log N) as O(N log N) > O(log N).
To conclude, the main aim of the article was to explain time complexity with log N without mathematical notation as there are many article with mathematical notations. The mathematically notation was used as proof for explanation. I hope, I explained log N used in time complexity in simpler way.